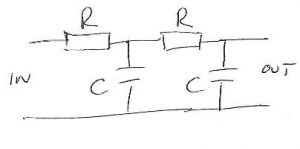
It eventually took a couple of days of odd minutes, including a Eurostar journey. The answer actually came earlier, but I couldn’t believe it had a ‘7’ in it – 2, √2 or π would have been more believable, but not 7 – so having started on the specific case with equal Rs and equal Cs, I moved to the more general case.

Thankfully remembering to:

• load the first stage with the second stage
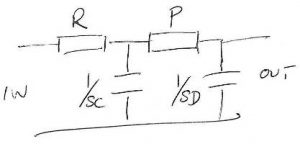
• use the s-domain 1/SC transform for capacitors
• do two separate equations either way from the mid-pint, then equate them
• simplify the immense mess

Out came: Vout/Vin = 1/(S²PRCD +S(RD+RC+PD)+1)

Which, amazingly, is that the internet said too 🙂

Substitute jω for S gave frequency response (ie, response with a constant-amplitude sine wave), but still including phase, and I was looking for an amplitude response, requiring the square root of the sum of the squares of the real and imaginary parts.

This is where a giant google-fuelled refresher course was needed…

during which this handy identity was discovered:

|H|=√( H(S⇒jω)H(S⇒-jω) )

So, replace S with jω in the above equation, and multiply that with the same equation, except with -jω replacing S instead.

This results in a massive mess, the typing of which here would take too much creativity.

Simplified, this produces:

1/√(1+ω⁴(PRCD)+ω²(R²D²+R²C²+P²D²+2R²CD+2PRD²))

Which seems to have the right combination of powers of ω and powers of the various RCs.

And agrees with the internet 🙂

Going back to the RCRC case, where P=R and D=C, a bunch of substitution yields:

1/√(1+(ωRC)⁴+7(ωRC)²)

That potentially pesky 7 was indeed true – assuming I did all of this correctly.

Working through an example (with 2πf substituted for ω) – giving 1/√(1+16(πfRC)⁴+28(πfRC)²), and comparing that result with a quick run on LTSpice, yielded similar-looking results.

Happy me.

I am guessing there is a way to get the same amplitude response with better or worse transient response by not having equal Rs and Cs, which could be found by doing transient response analysis as well, and then (guessing wildly) differentiating the ratio of one to the other, but I have hit my mathematical limit already….

BTW, someone identifying as Verbal Kint on StackExchange has posted a number of comments on ‘fast analytical circuits techniques’ (FACT), which seems to get to the right answers to similar questions in a quick and neat way (scroll down here, for an example).